摘 要

将激光雷达安置于坐标原点，利用激光雷达测定平面上目标点坐标（r，θ），实现对目标点的定位。为了避免激光雷达测量上的视野盲区，设置激光雷达在平面上 360° 旋转对空间进行扫描捕获目标点，为了消除激光雷达位于一固定点对目标点的定位，导致定位测量上数据的单一性，将激光雷达置于一移动平台，构建动态坐标系，测量与平台同平面目标点相对激光雷达位置的坐标（ri，θi），通过坐标转换，将多次测量的坐标平均值作为目标点的定位坐标值，实现对平面上特征点的定位，最后利用 MATLAB 进行数据处理绘图。

关键词激光雷达；扫描；移动平台；定位

为了描述空间物体的运动状态，需要确定其位置，对其定位，为此我们借用数学方法，建立坐标系，以坐标确定空间某点的位置，实现定位。空间定位无论是军事上的精准打击，还是民用上对目标的确定都有极其重要的意义和应用价值。本文利用激光雷达测距的原理，实现对平面上某点的定位。

1 激光雷达定位原理与方法

1.1 激光雷达测距原理

激光雷达是一种以激光作为载波探测目标位置的电子设备。激光雷达由发射模块、接收模块和信号处理模块三部分组成。激光雷达测距的基本原理是激光信号由发射模块发送出去，经过光学系统到达目标物，接收模块接收来自目标物的反射激光回波信号，在信号处理模块，回波经过处理进入到检测系统，最后获得目标物的距离信息。即

其中，L 是目标物的待测距离值，c 是空气中的光速，t 是发射接收往返期间时间值。

1.2 激光雷达定位原理与方法

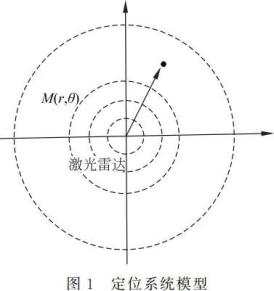
在平面上确定坐标原点建立极坐标系，那么定位平面上任意一点 M 的位置，需要知道 M 的坐标（r，θ），即 M 点到原点的距离以及与坐标轴的方位角，这样通过得到 M 点相对坐标系原点的位置信息而达到对 M 点的定位。

文中以激光雷达为中心，即坐标原点，利用激光雷达测距，同时记录扫描角度，所获得的目标点距离标准位置（激光雷达）的角度和距离的信息，经过坐标转化，将极坐标系中的（r，θ）转化为直角坐标系中的（x，y）。此过程为一次测量流程，为了提高定位精度，通过多个标准位置（即激光雷达不同位置为中心）对目标点位置测定，实现多次测量确定目标点位置。具体定位系统模型构建如图 1 所示：坐标原点 O 为激光雷达的位置，· 为目标点即待定位点 M 所处位置，激光雷达在坐标原点进行 360° 全方位旋转扫描，发射端对环境发射激光束进行采样，同时接收端接收从目标点反射回来的信号，信号处理端将接收信号与发射信号进行比较、检测、处理，最后根据匹配结果[1]，获得目标点 M 的位置信息（r，θ），经过坐标变换 x =r sinθ，y =r cosθ，得到点 M（x，y）。

实验中，为精确得到 M 的空间坐标，将测量系统激光雷达安置于一移动平台——可自由移动的平板小车上，车载激光雷达所处位置是定位系统坐标原点，这样就建立了一个以激光雷达为坐标原点的可移动的动态坐标系，位于移动小车上的激光雷达在不同位置对测量点的定位数据，就是一系列以激光雷达所处不同位置为坐标原点的不同坐标系下的对同一测量点的定位数据，如图 2 所示，激光雷达在位置 O 1 时，即 O 1 对点 M 定位测量，获得 M 1（r 1，θ 1），激光雷达移动到位置 O 2 时，即 O 2 对点 M 进行第二次定位测量，获得 M 2（r 2，θ 2），类推获得激光雷达移动到位置 Oi，即 Oi 对同一采样点 M 的 i 组测量定位数据 M i（ri，θi），应用 MATLAB 进行数据处理，将以 Oi 为坐标原点的坐标系下的定位测量数据 M i（ri，θi）转换为以 O 为坐标原点的坐标系下的 M（ri，θi），再取以 O 为坐标原点的坐标系下的 i 次测量值 ri 和 θi 各自的平均值作为以 O 为坐标原点的坐标系下的 M（r，θ）。即

最后为达成实时定位的目的，显示环节可以应用 frame Grabber 进行成像，实现在电脑上建图并定位。

这里需要说明的是，M（r，θ）是相对于 O 点的被定位点，为了便于描述，称 M（r，θ）为 O 系下定位点 M 点的位置，同理，称 M i（ri，θi）为 Oi 系下 M 点的位置，为了将 Oi 系下的M i（ri，θi）的坐标值转换为 O 系下的坐标值，需要确定 Oi 在 O 系下的坐标值，即移动的激光雷达在定位过程中自身的位置的确定。

下面是 Oi 在 O 系下位置的确定：首先在 O 系下，激光雷达位于 O 点，除了对目标点 M 进行定位外，根据待测地理环境条件，选取 i 个特征点即 Oi 对其定位，得到 Oi 在 O 系下坐标值 Oi（ri，θi），然后驱动小车使得激光雷达位于 Oi 再次以 Oi 为坐标原点对目标点 M 进行定位，得到 Oi 系下 M 点的定位坐标 M i（ri，θi），通过坐标转换得到 O 系下激光雷达位于 Oi 时的位置坐标 M（ri，θi）。

2 仪器与装置

激光雷达以及其各个部件构成如图 3 所示，激光雷达安置在移动平台上，整个测量系统如图 4 所示。驱动小车将激光雷达输送到测量位置后，启动雷达扫描，对目标点进行 360° 全方位旋转扫描开始测量。

3 数据测量与分析

3.1 测量系统定位准确性验证

测量系统定位是否准确是由其对所测点 M 到激光雷达的距离即以激光雷达为圆心的半径 r 和方位角 θ 的测量的准确性共同决定的。为了检验测量系统测距和方位角测量的准确性，在一平面上绘制极坐标，对测量系统分别进行测距和测角两种情况验证。

1) 相同角度下不同距离采样点的测量

取一张绘图纸，在绘制好的极坐标平面上选取标号为 A，B，C，D，E，F，G，H，I，G，K，L，I，J 共 10 个点，它们的方位角均为 180.0°，如图 5 所示。测量上述 10 个点与坐标原点即激光雷达的距离，对照为平面极坐标中以毫米尺所测距离为实际距离，计算测量值相对实际值的误差，测量结果如表 1 所示。

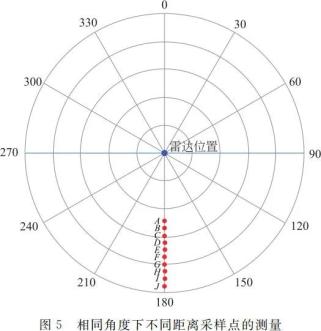
从表 1 可见，10 个样点的测量结果每次测量值与实际值的差距均略大于 20mm，本实验所购激光雷达的最佳测量范围为 5~12m，受绘制坐标纸张面积所限，所选取的采样点距离均小于 5m，不在激光雷达最佳测量范围之内，应该是导致测量误差较大的主要原因，从测量结果也可以发现随着测距的增加（A 点到 J 点），相对误差越来越小，如果待测点在 5~12m，估计实际距离与测量距离的差距和相对误差应该更小，测量效果会更好。

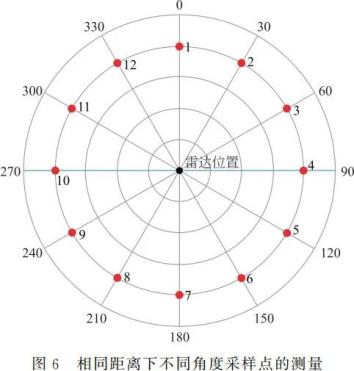
2) 相同距离下不同角度采样点的测量

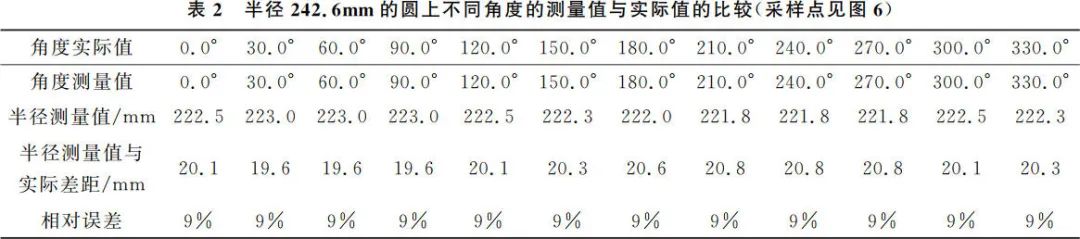
如图 6 所示，选取标号为 1~12 的 12 个相同半径 r=242.6mm 的采样点，即激光雷达与 12 个不同采样点的距离相同，都是 242.6 mm为实际距离，进行距离和角度测量，计算测量值相对实际值的差距及相对误差，测量数据结果如表 2 所示，角度结果保留小数点后 1 位的情况下，测量可以认为准确，误差可以被忽略，测量距离与实际值之间的差距在 20mm 范围摆动，测距相对误差保留一位有效数字时为 9%，12 个采样点一致。结合不同距离，相同角度下测量值与实际值的差距略大于 20mm（表 1），说明定位系统的误差主要来源于距离测量，方位角相对距离对定位结果的影响可以忽略不计。

3.2 对采样点动态测量

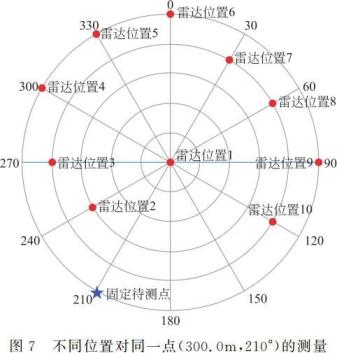
激光雷达位于不同位置对同一点 M（300.0，210°）（距离单位 mm，角度单位度°）进行定位。M 点和激光雷达位置如图 7 所示，雷达位置 1 为定位系统的坐标原点，（ri，θi）为激光雷达在位置 i 对固定点 M 的第 i 次测量时点 M 以激光雷达所处位置为坐标原点时的极坐标，（rj，θj）为激光雷达在位置 i 时，以 i 为坐标原点对 M 点所测到的坐标值（ri，θi）平移为已确定定位系统下的坐标值，即图 7 中以雷达位置 1 为定位坐标原点的坐标值。

图 7 雷达位置 1 为定位系统坐标原点，激光雷达在 10 个不同位置对 M 点进行定位，结果如表 3 所示。取 10 次测量值的坐标经过平移后的平均值

，作为 M 点相对于定位系统雷达位置 1 的定位。计算结果如下：

所以经过测量系统定位的 M 点的坐标为 M（280.4mm，210.0°）。定位点实际坐标 M（300.0mm，210.0°），测距误差 Δr=300.0－280.42≈20mm，角度误差为 0，与前面相同角度下不同距离采样点的测量以及相同距离下不同角度采样点的测量的验证结果相符，定位误差主要来自测距，约 20mm。

3.3 实例验证激光雷达空间定位能力

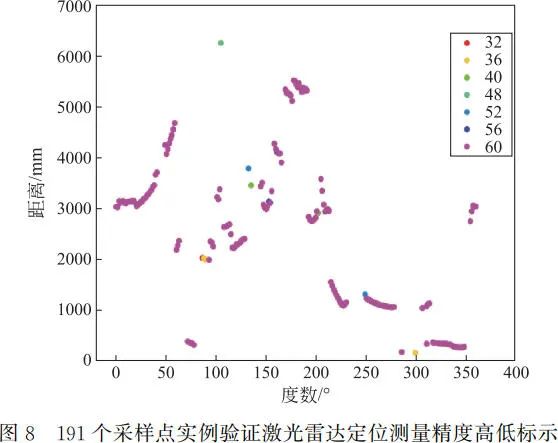
对该定位系统实例验证，将定位测量系统置于北林某教室的一个桌面上，对其周围物体——高于桌面的椅背 191 个样点进行定位（测量数据较为庞大，略去）。MATLAB 绘制测量样点（距离-角度-精度高低）分布图，如图 8 所示。图中数字表示测量精度高低，数字由小到大表示测量精度由低到高。例如角度（Angle）为 104.4°时，样点距离为 6258.5mm，精度数字标识 48。精度数字也就是激光雷达的强度，对于每个采样点，就是激光雷达回波的强度，一定程度上反映被扫描点的反射率，这个值越大，测量定位越好，精度越高。

4 结语

本测量系统可以较好地实现对空间样点实时定位；因为受到对照坐标系平面构建限制（小于 5m）,不在所购激光雷达有效测距的范围之内，定位距离误差均在 20mm 附近，可对测量系统进行校正，校正公式可以表达为 ρ =ρ测-c，c 由所购激光雷达确定，本定位系统中 c =20mm，定位角度误差为 0，精度高，效果好。

5 创新与拓展

目前，测距的方式多样，常见的是超声波测距与激光测距。与激光测距相比，发散角为超声波测距中超声波传感器的固有属性，对超声波传感器的实际测距精度[2]有一定影响，采用激光测距避免了因超声波波束发散所造成的障碍物较远时超声波传感器方向定位精度较差的缺点。不过激光雷达在发射系统和接收系统之间随着测量距离增大会存在视野盲区[3]，将激光雷达 360° 扫描，消除静态测量时出现的视野盲区。

激光雷达测距，因距离不同影响测量数据的精度[4]，引入移动平台装置后，建立了动态坐标系，获得不同位置下对同一采样点的多组测量数据，消除了激光雷达固定在一个位置时，静态测量所存在的一点定位测量数据单一的缺陷，实现了不同方位对同一点的定位；同时也消除了激光雷达因位置不同采样强度影响测量数据的精度。

如果将移动平台调换为一可在空间自由升降的装置，将激光雷达安装在此装置上，例如无人机，通过测量升降装置的高度，则可以实现空间三维定位和成像。

应用 MATLAB 进行数据处理和绘图，直观体现激光雷达定位的数据意义。

可以应用 frame Grabber 进行成像，实现电脑上实时定位建图。

参考文献

[1]张杰. 激光雷达原理系统软件设计[D]. 西安: 西安电子科技大学, 2010.

[2]穆卫谊, 张广鹏, 黄玉美, 等. 移动机器人的超声波传感器发散角标定及应用[J]. 仪器仪表学报, 2017, 38(3): 564-565.

MU W Y, ZHANG G P, HUANG Y M, et al. Calibration and application of ultrasonic sensor beam angle for mobile robots[J]. Chinese Journal of Scientific Instrument, 2017, 38(3): 564-565. (in Chinese)

[3]张一鸣. 超声波测距盲区研究的探讨[J]. 电脑知识与技术, 2020, 16(12): 256-258.

ZHANG Y M. Discussion of the research on the blind zone of ultrasonic ranging[J]. Computer Knowledge and Technology, 2020, 16(12): 256-258. (in Chinese)

[4]陈兆东. 高距离精度条纹探测和单光子计数复合激光三维成像研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.

作者简介: 马凤翔，女，北京林业大学副教授，主要从事大学物理、大学物理实验、电磁场理论的教学与研究，以及物理学在林学中的应用与研究工作，mafengxiang@bjfu.edu.cn。

引文格式: 马凤翔. 基于激光雷达平面实时定位研究[J]. 物理与工程, 2022, 32(1): 126-130.

Cite this article: MA F X. Research real time positioning on planar based on lidar[J]. Physics and Engineering, 2022, 32(1): 126-130. (in Chinese)