激光束腰和分布
为了获得高斯光束光学的精确原理和限制,有必要理解激光束输出的特性。在TEM(横模和纵模为0)模式下,光是从激光开始辐射,就像一个含有高斯横截发光剖面的完美平面波,如下图显示。高斯形状被激光内部的尺寸或者某种光学序列的限制光圈在某个直径处被截断。为了指定和论述激光光束的传播特性,我们必须给它的直径下一些定义。普遍被采用的定义是光束发光(最强烈)峰值,轴向或者数值的地方的直径衰减1/e2(13.5%)。
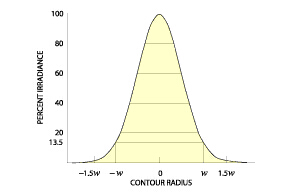
衍射效应使光在传播过程中向横向传播。因此它不可能有一个被精确校准的光束。激光光束的传播可以被纯衍射理论精确地预测。异常现象小到在这里可以统统不用去考虑。在非常平常的情况下,光束传播可以小到被忽略。下面的方程精确地描述了光束的传播,由此可以很容易地看出激光光束的能力和限制。
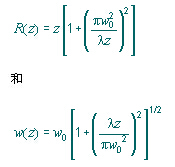
即使一个高斯TEM(横模和纵模为0)激光光束波阵面在某个平面可以保持非常的平坦,它也需要弯曲并且通过如下的公式传播
这里的z是当波阵面平坦时从平面上的传播路径,l是光的波长,w是当波阵面平坦时,在平面上1/e2发光轮廓的半径,w(z)是在波传播了距离z以后,1/e2轮廓的半径,R(z)是在波传播了距离z以后,波阵面的曲率半径。在z=0的条件下,R(z)是无穷大的,在某种有限的z的最小值内传播,并且当z进一步增大的时候,趋近于无穷大。Z=0平面标记了高斯腰的位置,或者表示波阵面是平坦的地方,这里w0叫做光束腰半径。
高斯TEM光束的发光分布按如下方式定义
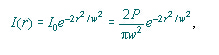
这里的w=w(z)和P是光束的总功率,在所有的相交的部分是等值的。分布形式的恒定性是对在z=0的时候高斯分布预测的特殊结果。如果统一的发光分布在z=0时刻被预测,z=∞时刻的形式将与贝塞尔公式给出的艾利斑(Airy disc)形式相似,这里z值中间的形式将变得非常复杂。
这里假定z远大于pw0 /l,因此1/e2发光轮廓渐渐逼近一个圆锥形的角半径
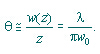
这个值是一个高斯TEM光束的远场角半径。圆锥的顶点在腰的中心位置,如下图所示。
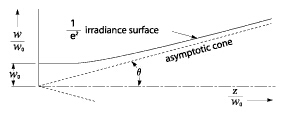
需要注意的是,在给定l值得条件下,不大可能表示出光束直径的变化和分布,在距离z作为一个独立参数运行时,W0,光束腰半径。
近场和远场的分别
不像常规的光束一样,高斯光束不是线性的分布。靠近激光的时候,分布角度是非常的小的。远离激光的时候,分布角如上描述接近渐进的限制。在瑞利判据范围,定义为光束半径通过2的平方根因素传播的距离,在下面式中给出
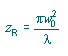
在光束腰(z = 0)的地方,波阵面更加平坦。同样地,在z = ∞处,波阵面也更加平坦(R(∞) = ∞).。随着光束从腰部传播,波阵面的曲率因此必须增加到最大值并且紧接着开始下降,如下图所示。Raleigh范围,考虑到在近场分布和中波段分布之间的区分线,是从波阵面曲率最大值腰部的距离。远场分布(数值查询激光器说明)必须在远大于ZR(通常大于10nbsp即足够)的时刻才能别测量。这是非常重要的区别,因为在一个光学序列中对点大小和其它参数的计算会在近场或者中场分布被使用时变得不准确。对于一个紧紧被聚焦的光束,从腰部(聚焦点)到远场的距离仅仅是几毫米或者更小。对于从激光直射光束,远场距离可以按米的数量级来测量。

转载请注明出处。









 相关文章
相关文章
 热门资讯
热门资讯
 精彩导读
精彩导读























 关注我们
关注我们




